[행위 패턴] Iterator pattern (이터레이터 패턴)
(원본출처 https://www.tutorialspoint.com/design_pattern/design_pattern_quick_guide.htm)
컬렉션이어떤 식으로 구현되었는지 드러내진 않으면서도 컬렉션 내에 있는 모든 객체에 대해 반복 작업을 처리할 수 있게 한다.
반복자 패턴은 Java 및 .Net 프로그래밍 환경에서 매우 일반적으로 사용되는 디자인 패턴입니다.
이 패턴은 기본 표현을 알 필요없이 순차 방식으로 컬렉션 객체의 요소에 액세스하는 방법을 얻는 데 사용됩니다.
반복자 패턴은 행동 패턴에 속합니다.
Implementation
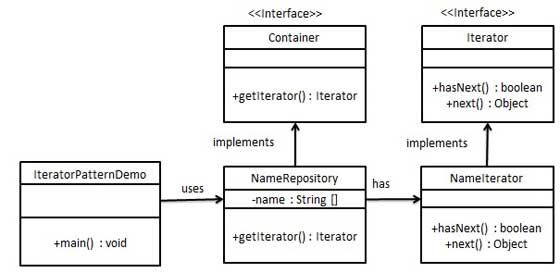
우리는 네비게이션 메소드를 설명하는 Iterator 인터페이스와 이터레이터를 다시 실행하는 Container 인터페이스를 생성 할 것입니다. Container 인터페이스를 구현하는 구체적인 클래스는 Iterator 인터페이스를 구현하고 사용하는 책임이 있습니다.
IteratorPatternDemo, 우리 데모 클래스는 NamesRepository를 사용하여 NamesRepository에서 컬렉션으로 저장된 Names을 인쇄하는 데 필요한 구체적인 클래스 구현을 제공합니다.
Step 1
인터페이스를 만듭니다.
Iterator.java
public interface Iterator { public boolean hasNext(); public Object next(); }
Container.java
public interface Container { public Iterator getIterator(); }
Step 2
컨테이너 인터페이스를 구현하는 구체적인 클래스를 만듭니다. 이 클래스에는, Iterator 인터페이스를 구현하는 내부 클래스 NameIterator가 있습니다.
NameRepository.java
public class NameRepository implements Container { public String names[] = {"Robert" , "John" ,"Julie" , "Lora"}; @Override public Iterator getIterator() { return new NameIterator(); } private class NameIterator implements Iterator { int index; @Override public boolean hasNext() { if(index < names.length){ return true; } return false; } @Override public Object next() { if(this.hasNext()){ return names[index++]; } return null; } } }
Step 3
NameRepository를 사용하여 반복자와 인쇄 이름을 가져옵니다.
IteratorPatternDemo.java
public class IteratorPatternDemo { public static void main(String[] args) { NameRepository namesRepository = new NameRepository(); for(Iterator iter = namesRepository.getIterator(); iter.hasNext();){ String name = (String)iter.next(); System.out.println("Name : " + name); } } }
Step 4
결과를 확인합니다.
Name : Robert Name : John Name : Julie Name : Lora
'Development > Java' 카테고리의 다른 글
| [행위 패턴] State pattern (스테이트 패턴) (0) | 2017.03.26 |
|---|---|
| [구조 패턴] Composite pattern (컴포지트 패턴) (0) | 2017.03.26 |
| [구조 패턴] Facade pattern (퍼사드 패턴) (0) | 2017.03.26 |
| [행위 패턴] Command pattern (커맨드 패턴) (0) | 2017.03.26 |
| [생성 패턴] Singleton pattern (싱글턴 패턴) (0) | 2017.03.26 |



